Map projections — coord

coord_map() projects a portion of the earth, which is approximately spherical, onto a flat 2D plane using any projection defined by the mapproj package. Map projections do not, in general, preserve straight lines, so this requires considerable computation. coord_quickmap() is a quick approximation that does preserve straight lines. It works best for smaller areas closer to the equator.

Both coord_map() and coord_quickmap() are superseded by coord_sf(), and should no longer be used in new code. All regular (non-sf) geoms can be used with coord_sf() by setting the default coordinate system via the default_crs argument. See also the examples for annotation_map() and geom_map().

Usage

coord_map(
  projection = "mercator",
  ...,
  parameters = NULL,
  orientation = NULL,
  xlim = NULL,
  ylim = NULL,
  clip = "on"
)

coord_quickmap(xlim = NULL, ylim = NULL, expand = TRUE, clip = "on")

Arguments

projection: projection to use, see mapproj::mapproject() for list
..., parameters: Other arguments passed on to mapproj::mapproject(). Use ... for named parameters to the projection, and parameters for unnamed parameters. ... is ignored if the parameters argument is present.
orientation: projection orientation, which defaults to c(90, 0, mean(range(x))). This is not optimal for many projections, so you will have to supply your own. See mapproj::mapproject() for more information.
xlim, ylim: Manually specific x/y limits (in degrees of longitude/latitude)
clip: Should drawing be clipped to the extent of the plot panel? A setting of "on" (the default) means yes, and a setting of "off" means no. For details, please see coord_cartesian().
expand: If TRUE, the default, adds a small expansion factor to the limits to ensure that data and axes don't overlap. If FALSE, limits are taken exactly from the data or xlim/ylim.

Details

Map projections must account for the fact that the actual length (in km) of one degree of longitude varies between the equator and the pole. Near the equator, the ratio between the lengths of one degree of latitude and one degree of longitude is approximately 1. Near the pole, it tends towards infinity because the length of one degree of longitude tends towards 0. For regions that span only a few degrees and are not too close to the poles, setting the aspect ratio of the plot to the appropriate lat/lon ratio approximates the usual mercator projection. This is what coord_quickmap() does, and is much faster (particularly for complex plots like geom_tile()) at the expense of correctness.

Examples

if (require("maps")) {
nz <- map_data("nz")
# Prepare a map of NZ
nzmap <- ggplot(nz, aes(x = long, y = lat, group = group)) +
  geom_polygon(fill = "white", colour = "black")

# Plot it in cartesian coordinates
nzmap
}


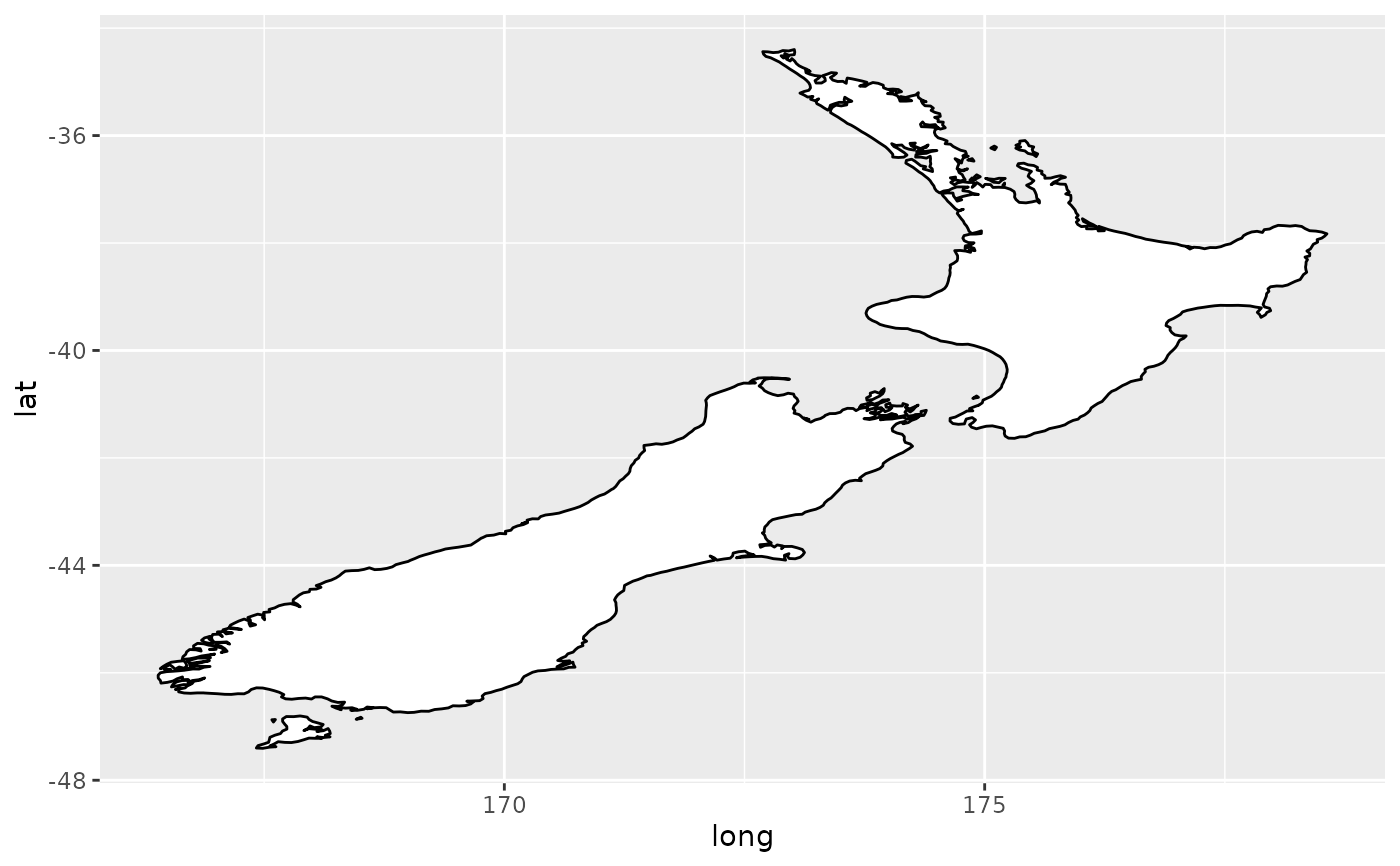if (require("maps")) {
# With correct mercator projection
nzmap + coord_map()
}


if (require("maps")) {
# With the aspect ratio approximation
nzmap + coord_quickmap()
}


if (require("maps")) {
# Other projections
nzmap + coord_map("azequalarea", orientation = c(-36.92, 174.6, 0))
}


if (require("maps")) {
states <- map_data("state")
usamap <- ggplot(states, aes(long, lat, group = group)) +
  geom_polygon(fill = "white", colour = "black")

# Use cartesian coordinates
usamap
}


if (require("maps")) {
# With mercator projection
usamap + coord_map()
}


if (require("maps")) {
# See ?mapproject for coordinate systems and their parameters
usamap + coord_map("gilbert")
}


if (require("maps")) {
# For most projections, you'll need to set the orientation yourself
# as the automatic selection done by mapproject is not available to
# ggplot
usamap + coord_map("orthographic")
}


if (require("maps")) {
usamap + coord_map("conic", lat0 = 30)
}


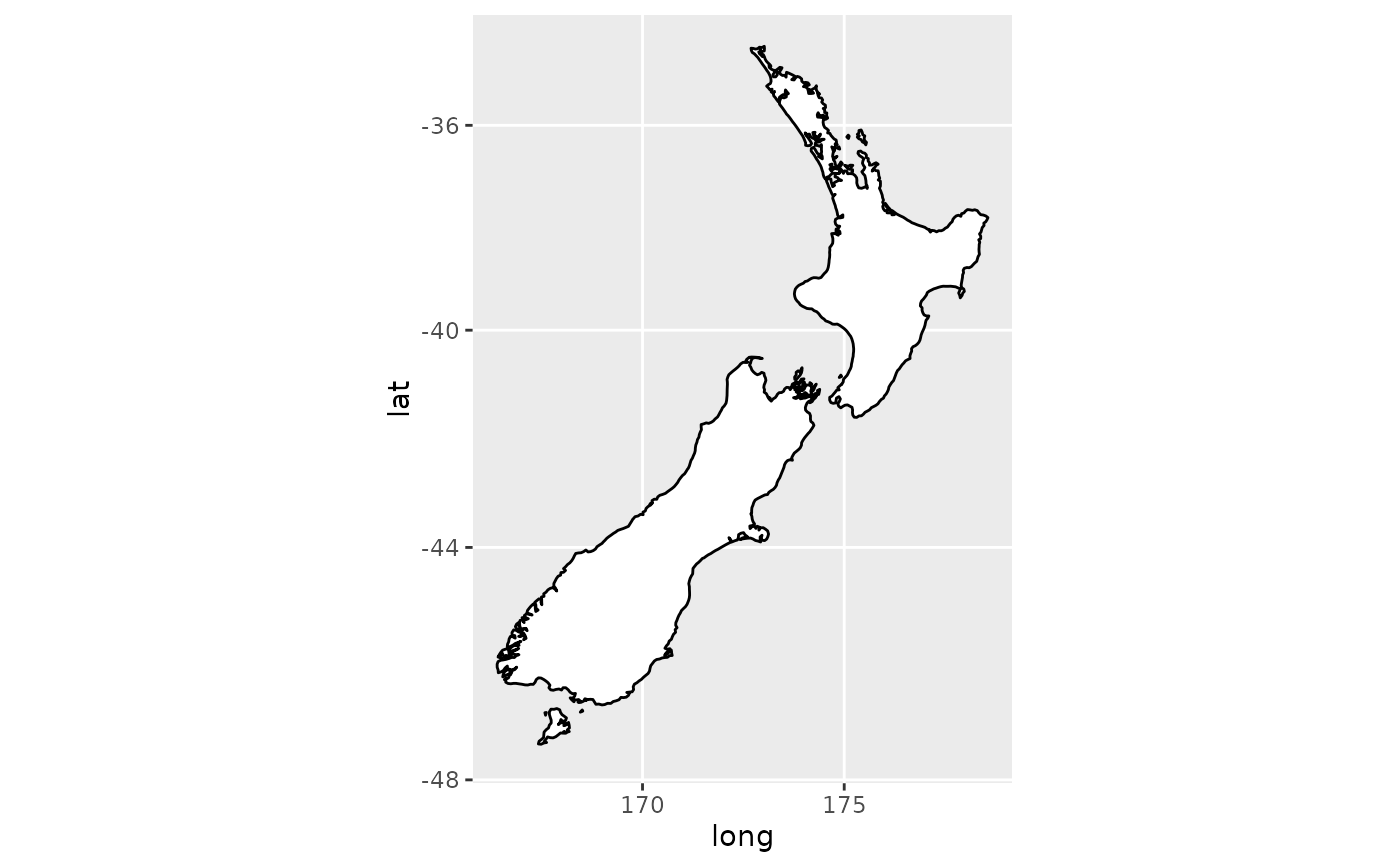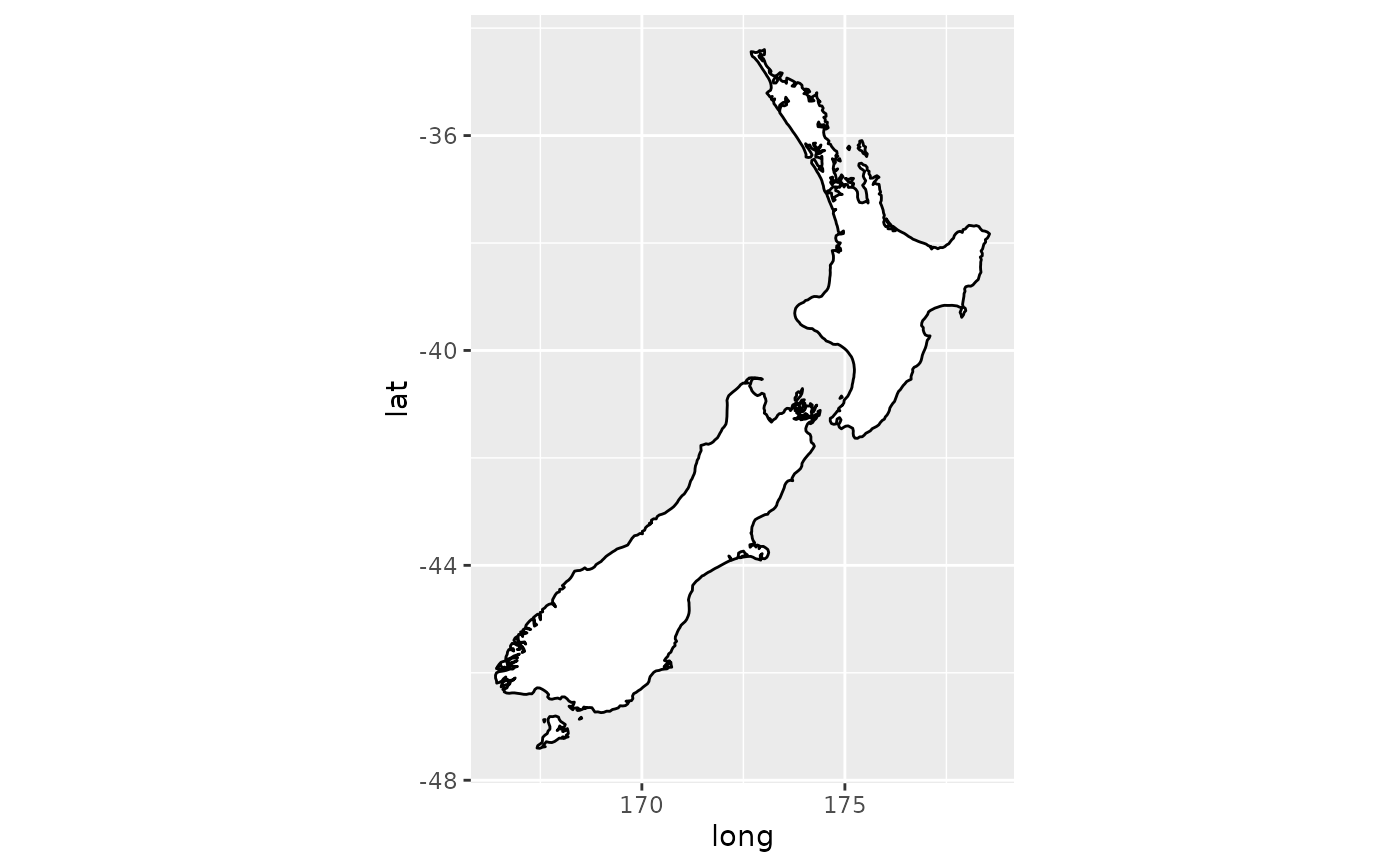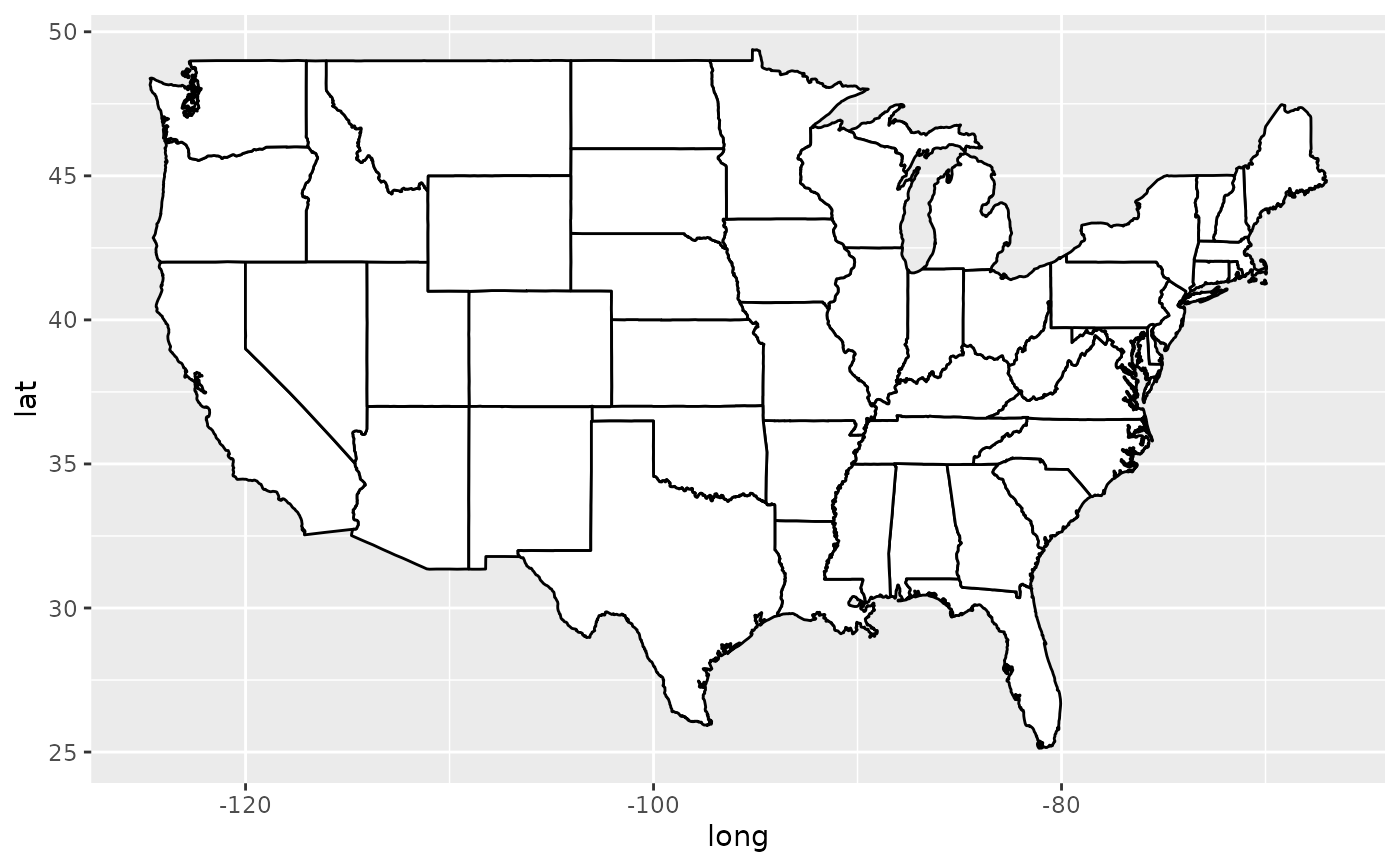
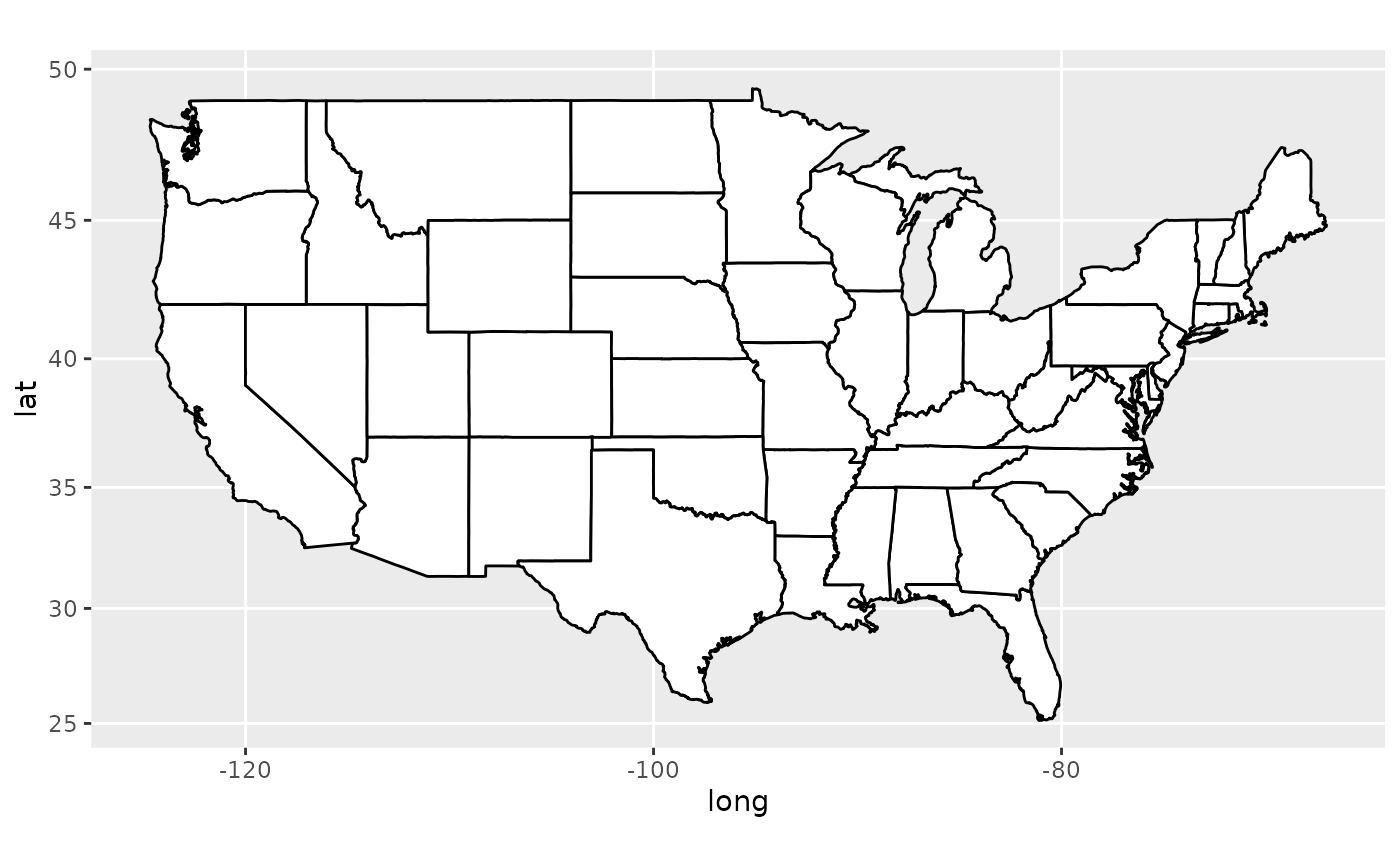
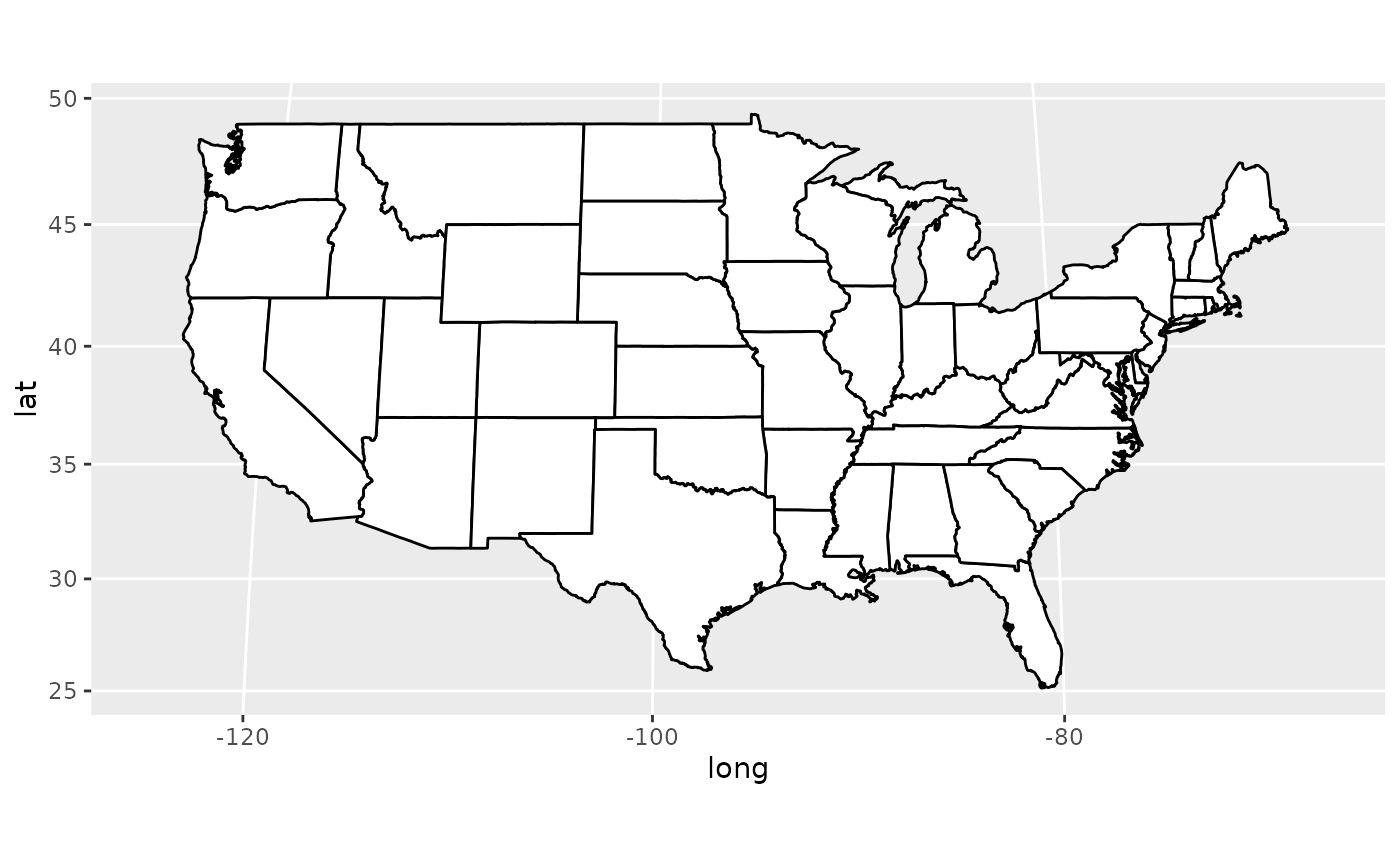
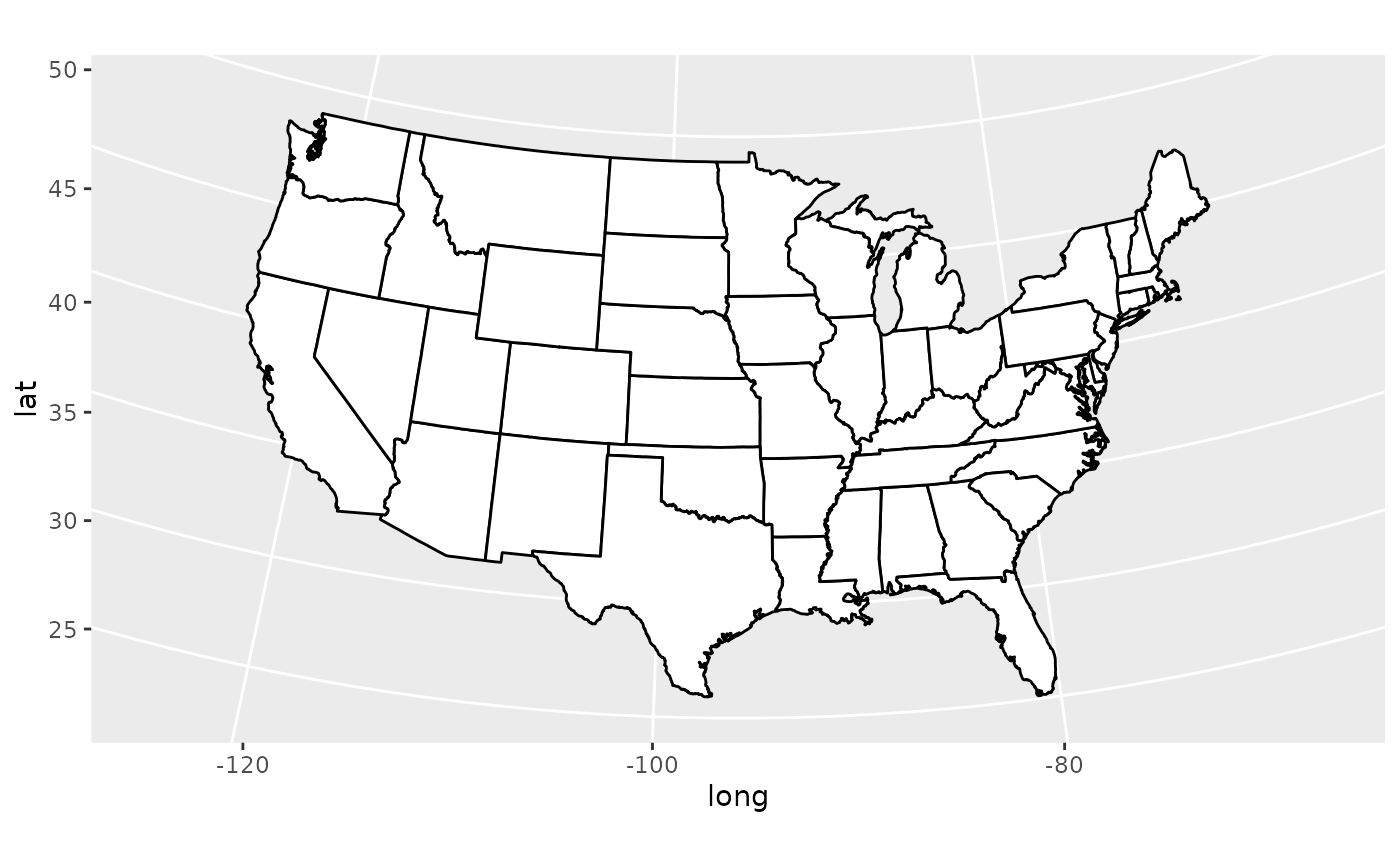
if (require("maps")) {
usamap + coord_map("bonne", lat0 = 50)
}


if (FALSE) {
if (require("maps")) {
# World map, using geom_path instead of geom_polygon
world <- map_data("world")
worldmap <- ggplot(world, aes(x = long, y = lat, group = group)) +
  geom_path() +
  scale_y_continuous(breaks = (-2:2) * 30) +
  scale_x_continuous(breaks = (-4:4) * 45)

# Orthographic projection with default orientation (looking down at North pole)
worldmap + coord_map("ortho")
}

if (require("maps")) {
# Looking up up at South Pole
worldmap + coord_map("ortho", orientation = c(-90, 0, 0))
}

if (require("maps")) {
# Centered on New York (currently has issues with closing polygons)
worldmap + coord_map("ortho", orientation = c(41, -74, 0))
}
}